• For any query, contact us at
  • +91-9872993883
  • +91-8283824812
  • info@ris-ai.com
RIS AI - Thesis Expert
Most Viewed Articles
Object Detection | Start up Profit Prediction | RealTime Eye Blink Detection | House Budget Prediction | Human Detection and Counting | Pencil Sketch of Photo | Predict Next Word with Python | Hand Gesture Recognition | Handwritten Character Recognition
  • Blogs >

  • Fake Currency Detection with Machine Learning

Fake Currency Detection with Machine Learning

Fake Currency Detection is a real problem for both individuals and businesses. Counterfeiters are constantly finding new methods and techniques to produce counterfeit banknotes, which are essentially indistinguishable from real money. At least for the human eye. In this article, I will introduce you to Fake Currency Detection with Machine Learning.

Fake Currency Detection is a task of binary classification in Machine Learning.

Now let’s get started with this task of Fake Currency Detection with Machine Learning. I will start this task by importing the necessary packages:

In [1]:
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import confusion_matrix

The dataset contains these four input characteristics:

The variance of the image transformed into wavelets The asymmetry of the image transformed into wavelets Kurtosis of the image transformed into wavelets Image entropy

The target value is simply 0 for real banknotes and 1 for fake banknotes. Let's read the dataset:

In [2]:
data = pd.read_csv('data_banknote_authentication.txt', header=None)
data.columns = ['var', 'skew', 'curt', 'entr', 'auth']
print(data.head())

       var    skew    curt     entr  auth
0  3.62160  8.6661 -2.8073 -0.44699     0
1  4.54590  8.1674 -2.4586 -1.46210     0
2  3.86600 -2.6383  1.9242  0.10645     0
3  3.45660  9.5228 -4.0112 -3.59440     0
4  0.32924 -4.4552  4.5718 -0.98880     0

Data Exploration :

Now let’s start exploring the dataset. First, I’ll check the data types and if there are any missing values ​​in the data:

In [3]:
print(data.info)

<bound method DataFrame.info of           var      skew     curt     entr  auth
0     3.62160   8.66610  -2.8073 -0.44699     0
1     4.54590   8.16740  -2.4586 -1.46210     0
2     3.86600  -2.63830   1.9242  0.10645     0
3     3.45660   9.52280  -4.0112 -3.59440     0
4     0.32924  -4.45520   4.5718 -0.98880     0
...       ...       ...      ...      ...   ...
1367  0.40614   1.34920  -1.4501 -0.55949     1
1368 -1.38870  -4.87730   6.4774  0.34179     1
1369 -3.75030 -13.45860  17.5932 -2.77710     1
1370 -3.56370  -8.38270  12.3930 -1.28230     1
1371 -2.54190  -0.65804   2.6842  1.19520     1

[1372 rows x 5 columns]>

We, therefore, have no missing values ​​in the data. We can now draw a pair diagram to get an overview of the relationship between all the entities. I will also colour the observations: blue for genuine banknotes and orange for counterfeit banknotes:

In [4]:
sns.pairplot(data, hue='auth')
plt.show()
Fake Currency Detection with Machine Learning

From this pair plot we can make several interesting observations:

  • Distribution of both variance and skewness appears to be quite different
  • There are clear linear and nonlinear trends in the input features.
  • Some characteristics seem to be correlated.
  • Some features seem to separate genuine and fake banknotes quite well

Now let’s check if our data is balanced against the target values:

In [5]:
plt.figure(figsize=(8,6))
plt.title('Distribution of Target', size=18)
sns.countplot(x=data['auth'])
target_count = data.auth.value_counts()
plt.annotate(s=target_count[0], xy=(-0.04,10+target_count[0]), size=14)
plt.annotate(s=target_count[1], xy=(0.96,10+target_count[1]), size=14)
plt.ylim(0,900)
plt.show()

/usr/lib/python3/dist-packages/ipykernel_launcher.py:5: MatplotlibDeprecationWarning: The 's' parameter of annotate() has been renamed 'text' since Matplotlib 3.3; support for the old name will be dropped two minor releases later.
  """
/usr/lib/python3/dist-packages/ipykernel_launcher.py:6: MatplotlibDeprecationWarning: The 's' parameter of annotate() has been renamed 'text' since Matplotlib 3.3; support for the old name will be dropped two minor releases later.
Fake Currency Distribution Target

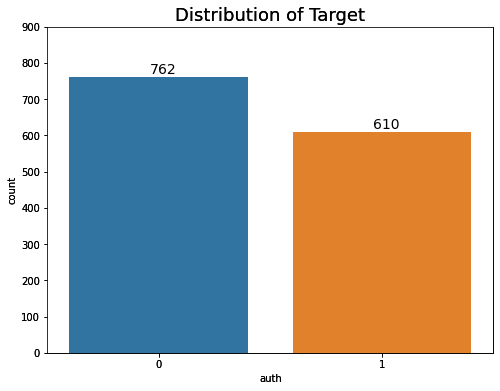
The dataset is fairly balanced, but for the binary classification task, we need to balance it perfectly. So let’s start preprocessing the data by doing just that.

Data Preprocessing :

In [6]:
nb_to_delete = target_count[0] - target_count[1]
data = data.sample(frac=1, random_state=42).sort_values(by='auth')
data = data[nb_to_delete:]
print(data['auth'].value_counts())

1    610
0    610
Name: auth, dtype: int64

Now we have a perfectly balanced dataset. Next, we need to divide the data into training and test sets:

In [7]:
x = data.loc[:, data.columns != 'auth']
y = data.loc[:, data.columns == 'auth']
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.3, random_state=42)

Now I will standardize the data by using the StandardScalar method provided by Scikit-learn:

In [8]:
scalar = StandardScaler()
scalar.fit(x_train)
x_train = scalar.transform(x_train)
x_test = scalar.transform(x_test)

Logistic Regression for Fake Currency Detection

Now, I will train and test our model for fake currency detection by using the Logistic Regressing Algorithm. Let’s first fit the data on the Logistic Regression model to train the model:

In [9]:
clf = LogisticRegression(solver='lbfgs', random_state=42, multi_class='auto')
clf.fit(x_train, y_train.values.ravel())
Out[9]:
LogisticRegression(random_state=42)

Now let’s test the accuracy of our model:

In [10]:
y_pred = np.array(clf.predict(x_test))
conf_mat = pd.DataFrame(confusion_matrix(y_test, y_pred),
                        columns=["Pred.Negative", "Pred.Positive"],
                        index=['Act.Negative', "Act.Positive"])
tn, fp, fn, tp = confusion_matrix(y_test, y_pred).ravel()
accuracy = round((tn+tp)/(tn+fp+fn+tp), 4)
print(conf_mat)
print(f'\n Accuracy = {round(100*accuracy, 2)}%')

              Pred.Negative  Pred.Positive
Act.Negative            187              6
Act.Positive              0            173

 Accuracy = 98.36%

Now let’s simulate the prediction of a single banknote.

In [11]:
new_banknote = np.array([4.5, -8.1, 2.4, 1.4], ndmin=2)
new_banknote = scalar.transform(new_banknote)
print(f'Prediction:  Class{clf.predict(new_banknote)[0]}')
print(f'Probability [0/1]:  {clf.predict_proba(new_banknote)[0]}')

Prediction:  Class0
Probability [0/1]:  [0.61112576 0.38887424]

Our model predicts that this banknote is real.

Search Article

Resources You Will Ever Need

Popular Searches